如果说Quant学习路径被视为苦难游戏《黑暗之魂》，那么Black-Sholes期权定价模型则可以被视为游戏初期的英雄古达，他是一个新人，一般都会劝新人退出。 如果你不懂 BS，那么在量化世界中你可能永远都是 BS。

作为诺贝尔奖得主模型，Black-Sholes 确实不是一件容易理解的事情。 在知乎上，我看到了各种大师，各种推导，各种公式。 在读者友好度上，人们似乎感受到了“知乎大佬们的恶意”。 这里先说一下BS模型，重点说一个简单易懂的。 核心推导详细呈现，即使是新手也能快速上手。

期权定价的逻辑

1.1 什么是选项？

BS 用于给期权定价。 什么是选项？ 用白话来说，类似于“赌大赌小”的赌博。 月初，一只股票价值5元。 你坚信到月底它的价格会达到10多元。 您打算购买 10,000 股，但您感觉口袋里没有那么多钱。 你必须等到月底发工资。 这时，金融世界为你提供了一个选择，让你即使没有钱也能实现投资愿望。

这是一个选项，一个指定期限的赌博证书。 如果这只股票月底真的能涨到10元以上，有了这张凭证，就可以以5元的价格买入该股票。 当然，您可以立即以市场价格出售。 但如果没有达到10元，这张券就没啥用了。 无论哪种情况，您都将承担购买此优惠券的费用，该费用相当于赌场的“入场费”。

因此涉及三个核心组件：

1 股票的初始价格就是上面提到的“5元”。

2 该期权的行权价格为上述“10元”。

3 如上所述，该期权的行权期限为1个月。

以这种方式看待选项是件好事。 它可以为“先知”提供一个“廉价”的选择，并以少量产生大效果。 但问题是，这东西值多少钱？

那么让我们来了解一下期权定价的故事。

1.2 定价逻辑

1.21 最简单金融产品的定价

首先，在给任何产品定价时，首先要考虑的是成本。 期权本质上是一种金融资产。 金融资产的成本是多少？ 很简单，是时候了。

今年的一美元不等于明年的一美元。 今天的一美元应该等于明年的 1*(1+r)，其中 r 是市场无风险利率。

最简单的金融产品定价：市场无风险利率为r。 如果你发行一年后支付1元的无风险固定收益理财产品，它的当前价格应该是1/(1+r)。 这就是所谓的一年期零息债券

逻辑：找到未来的现金流并将其贴现到当前。

1.22 期权定价逻辑

对于期权，假设当前价格为p，那么一年后的价格应为p*(1+r)。

这个p*(1+r)应该就是期权资产一年后给投资者带来的现金流。

那么问题来了？ 如何计算现金流量？

如果一年后股票价格确定为10元，那么我一定会以5元的价格买入股票，然后在市场上卖出，赚取10-5=5的利润。 那么这个期权就变成了一年后支付5元现金流的零息债券，它的价格应该是5/(1+r)。

但是，股价能达到10元吗？ 这是不确定的，这是一个概率游戏。

所以我们的定价逻辑是：

1 求出未来现金流，然后按照无风险利率折现，这应该就是期权的价格

2 现金流是一个概率事件。 需要找出各种现金流对应的概率，然后根据概率和金额计算总体现金流的期望值。

那么，困难就变成了计算各种期权未来带来的现金流量及其相应的概率。

二概率博弈（如何求未来的股价？）

我怎么知道股票未来涨到10元的概率？

2.1“神奇”的大数定律和中心极限定理

答案是你不知道，你只是假设你知道。 这个世界的统计学家会孜孜不倦、虔诚地告诉你，宇宙有两条亘古不变的神奇法则。 一是大数定律，二是中心极限定理。 这两个定理将解决概率的所有难题。

什么是大数定律？ 举一个非常简单的例子，抛一枚硬币，猜正面和反面。 如果你做的次数太多，变成一个很大的数字，你会神奇地发现正面和反面的数量逐渐接近总数的50。 %。

什么是中心极限法则？ 我们用一张非常简单的图来说明，如下：

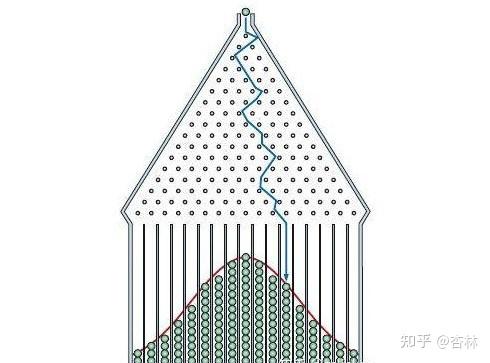
小球从上到下落下是一个（独立随机事件）。 最终，许多小球在“宇宙神奇法则”作用下落入网格中的形状，就是正态分布形状。 换句话说，我们扔了两个筛子，然后计算分数的总和。 显然，点数之和为12和2的概率应该是最小的，因为一定是两个筛子都是6或者1的情况，点数之和为6的概率会大很多，因为有点的多种组合（基本的排列组合问题）。 然后多次重复这个实验，最后看到从点2到点12的网格如上图，将出现的次数视为小球的数量。 您看到的是上面的正态分布的形状。

什么是正态分布？ 相信大家在初中的时候就应该接触过它。 它是高斯分布，具有期望和方差。 大家回顾一下也是有好处的。 这里暂时不写数学公式。 视觉理解是重复独立实验。 各种结果的分布是一条类似小山的曲线。

总结：

你说这么多是什么意思？ 这意味着统计学习告诉经济学家，准确预测股票价格的涨跌是没有意义的，因为趋势是随机游走的。 但如果你把股票价格的上涨和下跌视为一个独立的重复实验，你会发现上涨和下跌的结果应该符合正态分布。 对于这样的正态分布，可以通过大数定理计算期望值。 在这种情况下，你可以通过这个来预估股票价格，然后根据股票价格和期权的行权价格计算出期权的期望值。 现金周转。

接下来的问题是，如何将这两个神奇的定律应用到股票价格上呢？

2.2 布朗运动和几何布朗运动

此后，统计学家利用大数定理和中心极限法则百般推高股价。 他们的核心观点是股票价格遵循随机游走且不可预测。 所以说到随机游走，80年代出生的人应该会条件反射地想到高中时学过的布朗运动和花粉在水中的不规则运动。 没错，这就是布朗运动。

布朗运动实际上是指在一定的特征时间t内，布朗运动的变化满足均值为0、方差为t的正态分布。 好了，我们已经成功地将统计学的法宝运用到了股价上，但是似乎有一个问题，那就是股价不能有负值。 什么可以同时是积极的和消极的？ 股票的回报率还可以，因此统计学家认为股票回报率的变化是布朗运动。

那么，既然我们仍然需要股票价格来计算现金流，那么我们如何反映收益率对股票价格的布朗运动呢？ 答案是——几何布朗运动。 这个是从哪里来的？

2.21 为什么收益率呈正态分布，而股价呈现几何布朗运动？

首先，第一个问题是，如何从股价计算股票的收益率？

金融部门不使用算术回报，而是使用对数回报。

对数收益率的公式非常简单。 对数收益率是t时刻的价格除以当前价格，然后取对数：

r_t=ln(\frac{p_t}{p_{t-1}})

为什么使用对数回报？

最重要的好处是易于应用大数定律和中心极限定律。

例如，如果一开始股票价格为p0，那么一天后价格为p1，两天后价格为p2。

那么我们说一天后，它的收益率为r_{1}=ln(\frac{p_{1}}{p_{0}})，那么第一天到第二天的收益率为

r_{2-1}=ln(\frac{p_{2}}{p_{1}}) 那么就很简单了。 从第一天到第二天，收益率为r_{2}=ln({\frac{ p_{2}}{p_{0}}}) 数学上就是r_{1}+r_{2-1} 。 由于ln的加法规则：

ln[\frac{p_{1}}{p_{0}}]+ln[\frac{p_{2}}{p_{1}}]=ln[\frac{p_{1}}{p_{0 }}\times\frac{p_{2}}{p_{1}}]

好吧，假设股价已经过去了n天，n是一个很大的数字，因为每天的收益率变化是随机且独立的，那么这个故事就变成了一个类似于扔筛子的游戏。

回顾一下之前的大数定律，我们知道每天的预期收益应该收敛到它的均值，这里就是 \frac{r_{n}}{n} 。 关于中心极限定律，我们知道，如果将每一天的收益（筛子之和）相加，分布符合正态分布，收益之和为r_{n}。 也就是说，对于一只股票来说，它的长期回报率应该满足正态分布。

2.22 第二个问题是，从回报率到股价？

我们知道股价对收益率的表达，那么问题来了。 因为我知道从一开始到第n天的收益率是符合正态分布的，而这个收益率就是股价变化的对数。 的。 也就是说，一个变量的对数满足正态分布，那么我们说这个变量（股票价格的变化）本身满足对数正态分布。

因此，如果我们想把收益率故事变成股票价格故事，我们只需要找到一个描述股票价格的模型即可。 该模型中股票价格的变化满足对数正态分布。

然后聪明的数据科学家直接摆出了股价模型，然后向我们证明了股价的变化满足对数正态分布。 该模型称为几何布朗运动模型。

好的，模型如下：

\frac{dS(t)}{S(t)}=\mu dt+\sigma dB(t) 公式 1

S(t) 表示时间 t 时的股票价格。 满足上式的股价S(t)是几何布朗运动。

dS(t)表示在极小的时间dt内股票价格的变化。

学过微积分的同学立刻就会意识到，这是一个描述微观时间变化的微分方程。 显然，这个等式左边表示的是股价在一小段时间内的价格变化。

在等式右侧，dt 代表极小的时间量。 \mu 表示时间 t 内返回的均值或期望，\mu 表示时间 t 内返回的方差，B(t) 表示标准布朗运动，dB(t) 表示时间 t 内返回。 内标准布朗运动函数产生的增量。

下面证明利用该方程得到的股票价格符合对数正态分布，即股票价格的对数收益率满足正态分布的基本假设。

3、证明股票价格符合几何布朗运动，其对数收益率满足正态分布。

为了证明问题的核心：

1求出股票价格的表达式S(t)

2 然后求对数收益率表达式ln(\frac{S(t)}{S(0)})，然后分析其分布

3.1 S(t)的解

因为公式1涉及B(t)和dB(t)两项。 对于B(t)来说，布朗运动的轨迹是随机的，它在某一点的变化率无法计算，也就是说它是不可微的。 用数学语言来说，B(t)的导数\frac{dB(t)}{dt}无法计算。

因此，对于S(t)的求解，必须引入一个新的辅助器，这个辅助器就是著名的伊藤引理。

3.11: 伊藤引理和积分

我对伊藤引理的理解实际上是根据随机分析的特点，引入二次变分来重新解释泰勒展开式。

3.111 泰勒展开式有什么作用？

假设f(x)是x的函数，那么泰勒展开就是求df。 另一种写法是 f(x+dx)-f(x)

df=f'(x)(dx)+\frac{f''(x)}{2}(dx)^2+\frac{f'''(x)}{6}(dx)^3。 ..

如果f(x)是布朗运动B(t)的函数，我们只需要将上式中的x替换为B(t)即可，这将涉及

如何找到 (dB(t))^2，因为通常 (dx)^3 和更高阶...非常非常小，将约等于 0 并被省略。

3.112如何求(dB(t))^2？

答案是你不需要问。 这称为二次变分。 你只需要记住以下公式：

(dB(t))^2=dt , dtdB(t)=0, (dt)^2=0 公式2

关于二次变分原理请自行搜索维基百科。 这里不再证明。

综上所述：

这样，我们只需要把(dB(t))^2=dt带入泰勒展开式，删除高阶项，就可以得到伊藤第一引理：

df(B_{t})=f'(B_{t})dB_{t}+\frac{1}{2}f''(B_{t})dt 公式 3

3.12 高级伊藤引理

因为我们研究的期权是股票价格的导数，它与时间t和股票价格x都相关，所以这个函数是一个复合函数。

f(x,t)，如何为此找到 df ？ 也很简单，只需将两个小增量dt和dx带来的增量相加到复合函数f()即可。

根据经典微积分

df(x,t)=df(t)+df(x)

如果我们知道 x 是布朗运动 B(t)

将式3代入：

得到

df=\frac{\partial f}{\partial t}dt+\frac{\partial f}{\partial B_{t}}dB_t+\frac{1}{2}\frac{\partial^2f}{\partial x^2}(dB_{t})^2

联合二次变分 dB(t)^2=dt

获得伊藤引理的第二个引理：

df=(\frac{\partial f}{\partial t}+\frac{1}{2}\frac{\partial^2f}{\partial B_{t}^2})dt + \frac{\partial f}{\partial B_{t}}dB_{t} 公式 4

这里我就不解释伊藤引理、伊藤微积分和二次变分的推​​导过程了。 这里我只解释一下，这些直接可用的定理帮助我们求解S(t)的表达式。

好了，说了这么多，我们终于可以开始求解S(t)了。

3.13 求解S(t)

\frac{dS(t)}{S(t)}=\mu dt+\sigma dB(t)

为简单起见，使用 S 代替 S(t)

dS=\mu Sdt+\sigma SdB(t) 公式 5

引证期权衍生品是股票价格和时间的函数，即f(S(t),t)，那么df是基于泰勒展开式

df(S(t),t)=\frac{\partial f}{\partial S(t)}dS(t) +\frac{\partial f}{\partial t}dt+\frac{1}{2 }\frac{\partial^2f}{\partial S(t)^2}dS(t)^2 公式 6

（请复习一下前面公式2的内容，dtdB(t)=0，(dt)^2=0，所以在复合函数的泰勒展开中，涉及到上述两个方程的相关项都被视为约等于0 ）

这里我们知道dS(t)就是公式2

我们来求解(dS(t))^2，直接计算dS(t)*dS(t)

(dS(t))^2=\mu^2S(t)^2(dt)^2+2\mu\sigma S(t)^2dt dB(t)+\sigma^2S(t)^2(分贝(t))^2

这里，忽略比dt高阶的小量(dt)^2=0，dtdB(t)=0，根据二次变分(dB(t))^2=dt

推断

(dS(t))^2=\sigma^2S(t)^2dt 公式 7

好了，将公式2和公式7带入公式6，为了简单起见，将f替换为f(S(t),t)，最终得到：

df=(\frac{\partial f}{\partial t}+\mu S(t)\frac{\partial f}{\partial S(t)}+\frac{1}{2}\sigma^2S (t)^2\frac{\partial^2f}{\partial S(t)^2})dt+\sigma S(t)\frac{\partial f}{\partial S(t)}dB(t) 8 级方程式

剩下的就是找到这些偏微分项了。

因为我们仍然需要依赖对数收益率，所以令 f(S(t),t)=ln(S(t))

很明显：

\frac{\partial f}{\partial t}=0 (f() 与 t 无关), \frac{\partial f}{\partial S(t)}=\frac{1}{S( t)} , \frac{\partial^2f}{\partial S(t)^2}=-\frac{1}{S(t)^2}

将以上各项带入最终结果为

df=dlnS(t)=(\mu-\frac{1}{2}\sigma^2)dt+\sigma dB(t) 公式 9

通过积分我们可以很容易得到

S(t)=S_{0}e^{(\mu-\frac{1}{2}\sigma^2)t+\sigma B(t)} 公式 10

这样我们最终就得到了S(t)的表达式。

3.2 证明模型中股价的对数收益呈现正态分布

这一步是一个顺利的过程。

ln(\frac{S(t)}{S_{0}})=(\mu-\frac{1}{2}\sigma^2)t+\sigma B(t) 公式 11

在模型中，我们知道μ和sigma代表股票收益的期望和标准差，因此它们是已知的。

对于t，也是已知的。 公式 11 右边的前半部分是一个常数。

对于后半部分，σ B(t) 意味着将标准布朗运动乘以一个常数。

为了理解图像，我们将标准布朗运动放大或缩小 \sigma 倍，然后将其上下移动 (\mu-\frac{1}{2}\sigma^2)t 个单位。

所以毫无疑问B(t)是正态分布的。 经过上述操作后，仍然是正态分布。

因此，股票价格呈现几何正态分布，其收益率呈现对数正态分布。 证明完毕。

通过标准布朗运动 B(t)\sim \Phi(0,t)

然后 ln(\frac{S(t)}{S_{0}}) \sim \Phi((\mu-\frac{1}{2}\sigma^2)t,\sigma^2t)

四总结：

第一部分结束了。 核心内容是BS期权定价的核心模型——股票价格的几何布朗运动模型的讲解。

后来证明了该模型的合理性在于股票的对数收益呈现正态分布。 这应该与统计的神奇“宇宙法则”结合起来。

那么有了上面的基础，我们就可以用概率分布来解释期权未来会给投资者带来的现金流，进而对期权进行定价。